accusative

adjective

1. Grammar.
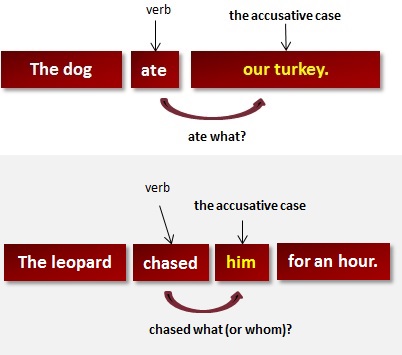
   1. (in certain inflected languages, as Latin, Greek, or Russian) noting a case whose distinctive function is to indicate the direct object of a verb or the object of certain prepositions.
   2. similar to such a case form in function or meaning.
2. Linguistics. pertaining to a type of language in which there is an accusative case or in which subjects of transitive verbs behave the same way as subjects of intransitive verbs.Compare ergative(def 2).
3. accusatory.

noun

4. an accusative case.
5. a word in an accusative case.
6. a form or construction of similar function.

adjective

1. grammar denoting a case of nouns, pronouns, and adjectives in inflected languages that is used to identify the direct object of a finite verb, of certain prepositions, and for certain other purposesSee also objective (def. 5)
2. another word for accusatorial

noun

3. grammar
   1. the accusative case
   2. a word or speech element in the accusative case

n.

grammatical case whose primary function is to express destination or goal of motion, mid-15c., from Anglo-French accusatif, Old French acusatif, or directly from Latin (casus) accusativus “(case) of accusing,” from accusatus, past participle of accusare (see accuse).

Translating Greek ptosis aitiatike “case of that which is caused,” on similarity of Greek aitiasthai “accuse.” Greek aitia is the root of both, and means both “cause” and “accusation,” hence the confusion of the Romans. A more correct translation would have been casus causativus.